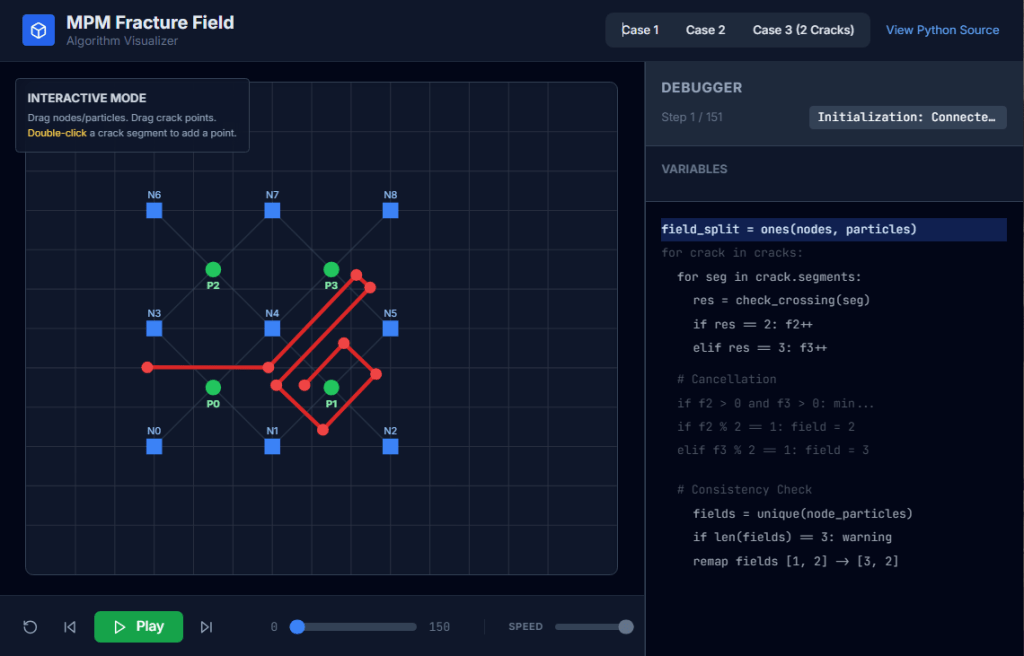
Check my github: MPM Field Visualizer
Line Crossing Algorithm:
The most time consuming, new calculation required for CRAMP is the linecrossing calculation in Task 2. It is important for this calculation to be optimal and precise. The only numerical difficulty occurs when a node lies very close to the crack path. In some line-crossing algorithms, numerical round off in this situation could result in two particles on the same side of the crack being labeled as being on opposite sides. The complementary problem of when a material point lines very close to a crack path never occurs because the contact methods keep particles from reaching the crack path.
A line-crossing algorithm in 2D based on signed areas of certain triangles solved the problem of nodes on cracks. For any three points, x1, x2, and x3, the signed area of the triangle with those vertexes is given by
Area = x1(y2−y3)+x2(y3−y1)+x3(y1−y2) (33)
This area is positive if the path from x1 to x3 is counter clockwise, negative if it is clockwise, and zero if the points are collinear. Using this signed area, the algorithm is as follows:
Subtask 1:
Before doing any calculations, determine if the rectangle defined by the particle (x1 = xp) and the node (x2 = xn) under consideration intersects the extent of the segment endpoints in the crack. If it does not, the line does not cross the crack and rest of the algorithm can be skipped for that crack.
Subtask 2:
For each crack segment with endpoints x3 and x4, calculate the sign of the areas of triangles (123), (124), (341), and (342) denoted as “+”, “−” or “0”.
Subtask 3:
The particle is above the crack if the signs are (−++−), (−++0), (0++0), or (−0+0). The first case is the most common; the other three correspond to the node being on the crack segment, on the start point of the crack segment, or on the end point of the crack segment, respectively. The cases where the material point is on the crack segment can be ignored. Similarly, the particle is below the crack if the signs are (+−−+), (+−−0), (0−−0), or (+0−0). All other combinations of signs indicate the line does not cross the line segment. In practice, many signed area calculations can be skipped. For example is the signs of (123) and (124) are (++), there is no need to evaluate the signs of (341) and (342) because the line can not cross the segment.
Subtask 4:
One complication is that a given xp to xn line might cross more than one segment in a single crack. In this situation, the crossing is ignored unless there are an odd number of crossings. To include this possibility, the previous two steps must check all segments in a crack before deciding if there is a crossing, but if Subtask 1 finds no intersection, the check for all segments in that crack can be skipped.
— Nairn (2003)
Particle-crack posision check:
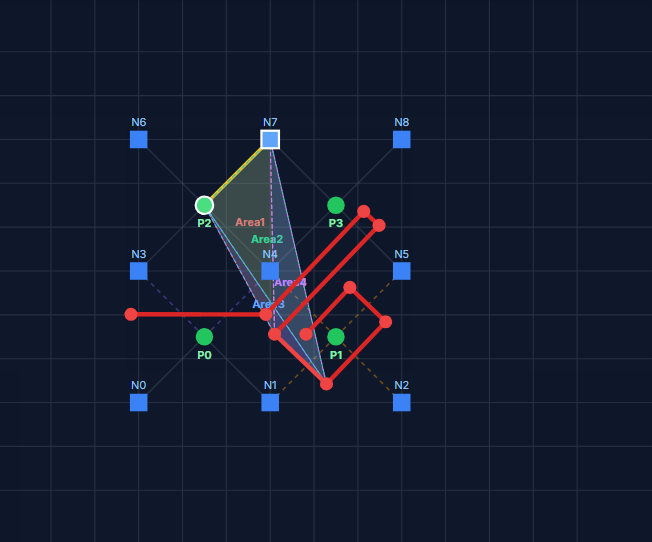
Node-crack stability check. (Sub stack 4)

Nairn JA. Material point method calculations with explicit cracks. Comput Model Eng Sci 2003;4:649–64.
Tito Adibaskoro, Stéphane Bordas, Wojciech T. Sołowski, Simo Hostikka,
Multiple discrete crack initiation and propagation in Material Point Method, Engineering Fracture Mechanics, Volume 301, 2024, 109918, ISSN 0013-7944, https://doi.org/10.1016/j.engfracmech.2024.109918.